The secret of Ms Dorobeth
Thursday, 18th October 2018 ◆ Abel's brother eats first honey links (5) MathsFor the purpose of filling out an in-development site with placeholder data, I decided to make a random name generator based on Markov chains. The goal was for it to create pronounceable and plausible names, but not necessarily real names.
First, a bit about Markov chains. If you have a set of "states", a Markov chain simply describes the probability of moving from any state to any other state. For example, imagine we have a mood lamp which changes colour every second according to the following Markov chain:
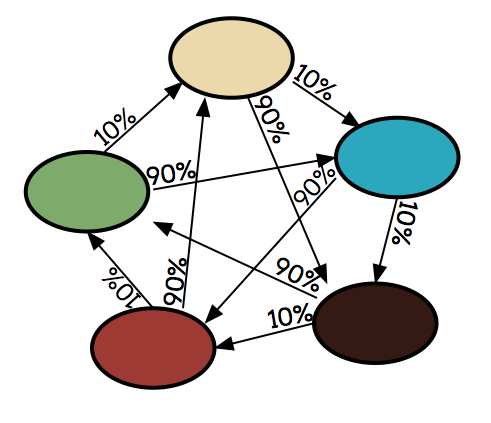 Markov chain for a mood lamp
Markov chain for a mood lamp
This (overcrowded) diagram tells us that if the lamp is showing green, we have a 10% chance of moving to beige, and a 90% chance of moving to blue. The probability of jumping from green to red is 0% (it won't happen), and this is indicated by not drawing an arrow. Note that the sum of all the probabilities of leaving a state is 100%.
To generate names, I made a Markov chain in which each time you jump to a new state, you add an extra letter. That is from a state with N letters, you can only jump to a state with N+1 letters (the probability to jumping to a state with any other number of letters is 0.) This is what a portion of that Markov chain might look like:
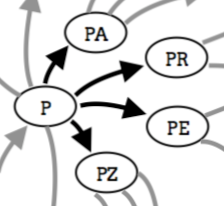 Markov chain for names
Markov chain for names
There is also a special 'letter' which indicates the end of a name. I'll call it "$". For example, "PATRICK" would have a non-zero chance to jump to "PATRICK$", which would mean our name is complete and that our name is "PATRICK".
In order to choose suitable probabilities, I downloaded the results from the US census of 1990 and trained the Markov chain on them.
To demonstrate how I trained the chain, let us imagine the census only contained the following 5 names:
MICHAELA
MABLE
MARGARET
HARRIET
SHARONWith this sample, we see that the first letter can either be "M", "H" or "S". "M" is more common than the others, and so should have a higher probability of being chosen. Thus our chain would assign the probability of jumping from "" to "M" as 60%, "" to "H" as 20% and "" to "S" as 20%.
In a similar fashion, we assign "M" to "MA" as ~67% and "M" to "MI" as ~33%. This means we won't generate a sequence of letters which isn't seen in real names. Jumping from "M" to "MQ", for example, has probability 0 here because it is not a sequence which is in the source data.
When training the Markov chain, I decided to use only the previous two letters to inform which letter to pick next. For example, "...HA" can go to:
- "...HAE", as seen in "MICHAELA"
- "...HAR", as seen in "HARRIET" or "SHARON"
Where "..." represents any sequence of letters. Since I'm only using the last two letters to decide which letter to pick next, even though "SHA" is always followed by "R" in our source data, "SHAE" could still get generated. If you could only do sequences which are seen in the source data, you will always end up with a real name, whereas I want to be able to generate a large number of plausible names from a potentially small sample set. I'm essentially encoding the rules of what is and isn't a valid sequence of pronounceable letters in the Markov chain.
Finally, in order to avoid infinite loops, I impose a maxium size of 10 letters in the name. Thus, the probability of jumping from any 10 letter name, "...", to "...$" is 100%.
If we do this for first names and last names separately, let's see what kind of output we get:
JEAH BARTINCH
ARKLISHA MOON
JAMY SARMAND
CHRITA BELDBURM
ELEY SWAREINO
DOROBETH HOLDS
ROBIO HULL
MARIS CALATAN
DAVID TONELL
KENNEY MONNISLE
GERREY ROBBOLLEThere are some real names (like "DAVID"), but mainly we have lots of exotic names. Let's look at "DOROBETH HOLDS". How does her first name get generated?
"DORO" can get produced because "DOROTHY" exists in the census. Then, from "RO" (the last two letter of the name), we can jump to "ROBE" (for example, in "ROBERTA"). Likewise, from "BE" we can complete "BETH".
This is a bit like how parakeets talk. Are the brains of birds Markov chains? Are ours?
You can look at a list of randomly generated names here.
Edit: 9th December 2022
- Added an endpoint which returns JSON, making a bit easier to integrate with other processes
- Cached the Markov chain, so it returns much quicker (previously it was creating the whole chain with each request)
I'm still using this tool often, whenever I need a random name generated!


Comments
There are no comments yet.