Fractals in polygons
Friday, 12th June 2020 ◆ Rex Imperator gets in a mess, romantically? (8) ◆ Comments (1)I saw a tweet last week from Matt Henderson with a simple algorithm for building a fractal pattern inside a hexagon. I have embedded the tweet at the end of the post - you should go see it. The algorithm goes thus:
- Plot a point inside a polygon
- Create a triangle with that point and a randomly selected edge of the polygon
- Plot the centre of that triangle
- Go back to step 2
The original tweet did this using a hexagon and the centroid, but I was curious what the patterns would look like in other polygons and types of centre, so I made a little toy in which you can play around with those options.
I have implemented the four most common triangle centres: the incentre, the centroid, the circumcentre and the orthocentre.
The incentre is where the angle bisectors cross. An angle bisector is a line which divides an angle into two equal angles.

The centroid is the mean of all three points: add up all the x coordinates and divide by three, then do the same for y. Alternatively, it is the "centre of mass" of the triangle.
The circumcentre is where the perpendicular bisectors cross. A perpendicular bisector is a line which intersects an edge at right angles, and divides that edge into two equal lines. It can also be described as the centre of a circle whose circumference contains the three vertices of the triangle.

Unlike the centres above, the circumcentre may not lie inside the triangle. This can be seen especially clearly when the triangle has one large angle.
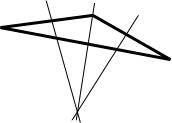
The orthocentre is where the altitudes intersect. An altitude is the line from one vertex to the opposide edge, such that it intersects that edge at right-angles.

Again, the orthocentre doesn't necessarily lie inside the triangle.
The most interesting thing I saw is that a triangle with centroids produces a mini Sierpinski triangle!

Another interesting result is that doing this with the circumcentre plots out the centre of the polygon. For polygons with an even number of sides, it bisects the edges. For those with an odd number of sides, it bisects the angles.
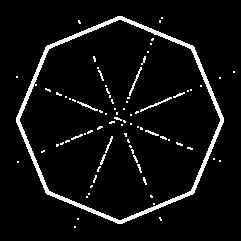
For the orthocentre, it seems most of the drawing is done outside the canvas so I saw nothing of note. Maybe with a bigger canvas some interesting pattern would be revealed... if you try it out, let me know!
The drawing is done using PIXI.js. The canvas I'm using is only 256 x 256, which is much lower resolution than in the original tweet:
a simple and random process that creates an intricate and structured fractal pattern. At each step, pick a random edge to form a triangle, and the next point is the center of the triangle. pic.twitter.com/yLxmdZQCWY
— Matt Henderson (@matthen2) June 5, 2020


Comments
I love your in-depth investigation. It's cool that that centroid on any shape seems to create a sierpinski-like for that shape.
One thing I noticed after leaving it running for a while is that the circumcentre appears to create the inverse image of the orthocentre. https://imgur.com/a/Whz6s1a If you squint :P